Lowell Christensen, VP Engineering
TruTech Specialty Motors
Magnetics 2013 Orlando Florida Feb 8 & 9, 2013
This presentation will discuss the effects of changing the Flux density in the airgap of a Permanent magnet Brushless Permanent Magnet Servo motor on the overall motor performance. The air gap flux density is the major parameter that a motor designer will base a motor design on. This presentation will show that the motor magnetic circuit designs can be modified to allow maximum motor performance with lower energy grade magnetic materials than the present high energy rare earth magnets. The higher energy rare earth magnets used have always had a higher cost but now that some of the rare earth components have become harder to source, the need to use mid range energy magnet materials could become necessary. This has started a trend to mix the various magnet materials which can change the magnet performance to values that were not available in the past as single magnet materials. The airgap flux density in this presentation will be varied from 3 KG to 9 KG and the effects of this variation of the airgap flux density on permanent magnet motor designs will be shown.
The designs used in this presentation will have the flux density of the iron laminations kept constant with the flux density of the iron in the lamination teeth kept at 14 Kg and the flux density of the lamination back iron kept at 13 KG. This means that as the lamination iron thickness of the teeth and back iron will need to get larger as the flux density is increased to keep the flux density constant. This will cause the slot area for the wire to decrease as the flux levels in the air gap increase. The effect of this is shown in Figure 1. The diagram below shows a motor with a low airgap flux density resulting
Figure 1 – Lamination Changes as Airgap Flux Density Changes
in small iron thicknesses and a large area for the copper windings. The diagram on the right shows a motor with a high airgap flux density with thick iron cross sections and a small area for the copper windings. The number of turns in the winding is directly proportional to the airgap flux density when the stator diameter and length are kept the same. This can be shown from the equation for voltage generated in a coil passing thru a magnetic field, V = B * L * R * N, where V is voltage, B is flux density in Tesla, L is the length of the airgap in meters, R is the radius of the airgap in meters, and N is the number of conductors in the field. This shows that if R and L are kept constant, the number of turns will decrease as the airgap flux density is increased when the voltage generated is kept constant in the same motor design of airgap length and radius. The effect of decreasing area and decreasing turns in the slot shows a relationship of the two that will be looked at in the examples given in this presentation.
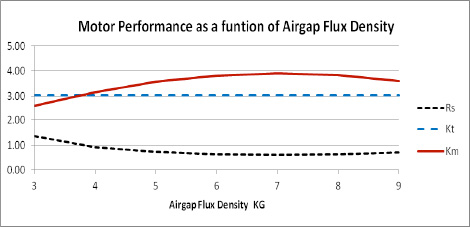
The motor performance can be measured in several ways for these comparisons. The most direct way is to measure and plot the motor constant which is defined as the motor torque constant divided by the square root of the stator resistance. If the top and bottom of this equation are multiplied by current then the equation would give the motor constant as the torque delivered by the motor divided by the square root of the power term I^2*R. By playing around with these parameters of torque and dissipated power loss, it can be shown that the motor constant is effected by the airgap flux density and the amount of copper in the slots along with the motor stator OD ,ID and length. Since the desired motor performance would be to get the most torque out of a motor with the lowest power loss, the Km will be at a maximum when the Kt value is high and the resistance is low.
Figure 2 – Example of Motor performance as a function of airgap flux density
Both the turns per coil and wire sizes are fixed whole numbers. This will cause the motor Kt to vary from the desired value and would skew the data. This presentation will use fractional values for the turns and wire sizes to keep the Kt a constant value at any value of airgap flux density. This will show the theoretical information for comparisons but would not represent actual values obtained in a true design. The comparisons done in this presentation will plot the motor constant as a function of the airgap flux density. It will be shown that the maximum value of the motor constant is not always at the highest levels of air gap flux density.
The results of varying the airgap flux density in a permanent magnet brushless motor with the ratio of the OD to the ID of 0.6 is shown in figure 2. As the airgap flux density is increased the resistance will start to drop but the lamination geometry due to keeping the lamination flux densities constant will override the decrease of the turns needed and the resistance will start rising again. It can be seen that the motor Km will start out increasing with the increase of airgap flux density and in some cases will decrease at the higher flux density levels. This would say that the best airgap flux density is not always the highest value that can be achieved with high energy magnets.
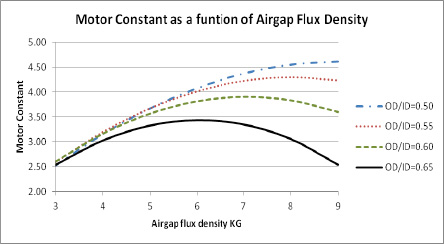
Another factor that affects the motor performance is the ratio of the stator OD to the stator ID. As this ratio changes, the effect on the motor constant will peak at different levels of the airgap flux density when the motor torque constant is kept at a constant value. This effect will first be shown on a motor with a stator OD of 3.6 inches and a stack length of 1.5 times the stator OD. The Torque constant in this example was kept constant at 3 Lb-In/A and the wire fill was kept constant at 40%.. This was chosen because it since it would give a motor about 4 inches or 100 mm in diameter to run an a 170 volt DC buss. This would be about an average size for a servo motor. The shaft diameter was small enough so that the rotor back iron would not be saturated at the highest level of the air gap flux density. This will keep the rotor geometry effects out of the example and keep the comparison to the airgap and stator. Figure 3 shows the effect of the motor constant as the stator OD to ID ratio is varied from 0.5 to 0.65.
Figure 3 – 3.6 inch diameter cylindrical motor
In the OD to ID ratio of 0.5 the motor constant is increasing as the motor airgap flux density is increasing but is starting to flatten out at about 8 KG in the airgap. There is very little change in Km above 8 KG but there are significant changes in below the 8 KG airgap flux density. If the OD to ID ratio is changed to 0.65 the motor constant will peak at a value of about 6 KG. At this OD to ID ratio, there is very little change in the motor constant from 5 KG to 7 KG but a large drop in the motor constant above and below these values. The other curves show different ratio values and show that the peak of the motor constant varies as the stator OD to ID ratio is changed.These plots show that the lower energy type magnet materials will work just as well as the high energy materials in designs made for the lower values and will be a lower cost material and will probably be a material that is more readily available.
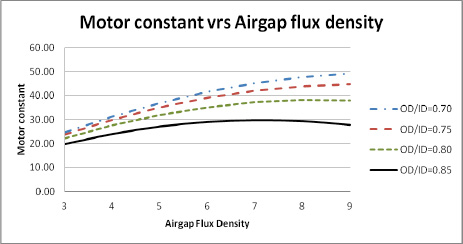
The first question that this may raise is, what will be the effect of the airgap flux density in larger diameter thin ring torquer style motor? These motors are usually used as direct drive and have a lot lower speed requirements. This gives the motors a very high Ke and Kt values. The larger diameter and the low speed allows a lot higher pole count then the cylindrical motors. Since the diameter is large the motors would tend to have a lot higher OD to ID ratio than the cylindrical style brushless motors. The effects of the air gap flux density will be checked on a 14 inch diameter pancake motor with a 2 inch stack length and a 16 pole 48 slots magnetic circuit. The results of this are shown in Figure 3. This shows that for an OD to ID ratio of 0.7 the motor constant Km is still rising. As the OD to ID ratio is increased from the 0.7 ratio to a 0.85 ratio the motor constant starts to tail off and drop at the higher airgap flux density levels. For the OD to ID ratio of 0.85 the motor constant will peak at about 7 KG in the airgap. There is little change in the motor constant from the 6 KG to 8 KG level and any air gap flux density in this range would give about the same results. The motor constant shown in Figure 3 is in In-Lb/square root of ohms for units.
Figure 4 – 14 inch OD pancake Motor
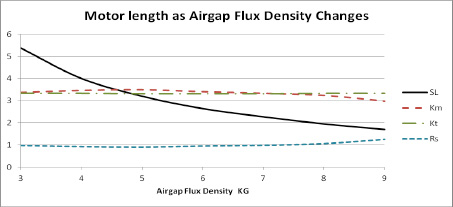
Another factor to investigate is the change in motor volume as the airgap flux density is increased. It has always been known that the higher energy rare earth magnets give a smaller motor than using lower energy ferrite magnets but the effects between these two materials will be checked. The effects of the air gap flux density on motor volume will be shown using an example that has the same motor diameter but the length changing with the air gap flux density. An example of volume could also be shown by changing the diameter or changing both the diameter and length as the airgap flux density is changed. The example of a constant diameter motor shows the overall effects and will serve as the example here. The example used here is a 4 pole 12 slot 3.6 inch diameter motor with the Kt kept constant at3.3 Lb-In/A and the wire fill kept constant at 40 %. Other factors kept constant were the rotor OD, the rotor ID and the magnet angle. Figure 4 shows the effects of the change in length resulting in a volume change as the airgap flux density varies from 3 KG to 9 KG. The data used for this graph was generated on motor design software using common magnet materials to get an air gap flux density close to the value needed, then changing the magnet thickness and airgap thickness to reach the value of airgap flux density needed. Next the tooth width and stator lamination back iron thickness to keep the tooth flux density at 14 KG and the back iron flux density at 13 KG for each calculation. Then the motor length was changed to get the Ke to a constant value of 39.5 volts per KRPM. The winding was kept constant at 26 turns per coil and the wire fill was kept at a constant value.
Figure 5 – Changing the stack length as the Bg changes
The results in figure 5 show that the motor Kt stayed constant as the flux density increased from 3 KG to 9 KG. The resistance took a slight dip initially as the airgap flux density increased but then started to rise as the stack length got shorter. The motor constant rose slightly as the resistance initially dropped, but then started dropping as the resistance started rising. The change in resistance in this example is due to the variation in stack length. This example has the same outer diameter in each case but the stack length is varying. The resistance due to the end turns will become a higher percentage of the total resistance as the stack length is shortened. This results in the slight increase of the resistance as the stack gets shorter. If the motor diameter had decreased with the shortening of the stack the Km and the resistance would have remained flat. The change in length shows a large decrease at the low airgap flux levels but tends to flatten out more at the higher airgap flux density levels. This shows the effect of motor volume decreasing with the increase of the airgap flux density.
Summary and Conclusions
The airgap flux density is a very important consideration when designing a permanent magnet servo motor. It was shown that either the motor size can decrease as the airgap flux density was increased or the motor output torque rating can be increased as the airgap flux density is increased. This presentation has also shown that geometrical parameters of the stator design can have a very large effect on finding the optimum airgap flux density. The ratio of the outer diameter to the inner diameter of the lamination will have an effect on the optimum airgap flux density. As the airgap flux density is increased, the amount of iron needed in the lamination also increases. This will decrease the slot area needed for the stator winding. The other factor is that as the airgap flux density is increased, the number of turns needed for the winding will decrease. The decrease in slot area will depend on the ratio of the OD of the lamination to the ID of the lamination along with the tooth width. The combination of this along with the number of turns required will make a optimum flux density for the motor air gap. The variation of the ratio of the OD to ID of the lamination was plotted against various airgap flux densities to show how the optimum airgap flux density can vary. It was also shown that the optimum ratio will change depending on the style of motor in design. The thin ring torque style motors with large pole counts will have the optimum OD to ID ratio at a larger value than the smaller diameter long motors with lower pole counts. This is important since the very high energy magnets are becoming more expensive and some of the rare earth materials used in the magnets are becoming harder to source. New magnet parameters are becoming available by mixing magnet materials in the production of magnets. This will make new magnets available that can give the mid range of airgap flux densities.